Introduction
The set command is a built-in Linux shell command that displays and sets the names and values of shell and Linux environment variables. On Unix-like operating systems, the set command functions within the Bourne shell (sh), C shell (csh), and Korn shell (ksh).
In this tutorial, you will learn what the set command is and how to use it.

Prerequisites
- A system running Linux.
- Access to a terminal/command line.
Linux set Command Syntax
The general syntax for the set command is:
set [options] [arguments]Options
In the context of the set command, [options] are settings or flags that are set or unset in the Bash shell environment. Use it to influence the behavior of defined shell scripts and help execute the desired tasks.
- Set an option by using a minus sign (
-) followed by the appropriate option. - Unset an option by using a plus sign (
+) followed by the appropriate option.
Arguments
[arguments] are positional parameters and they are assigned in order with the following parameters:
$1$2- ...
$n
Not specifying any options or arguments causes the command to print all shell variables.
Exit Values
The set command has three exit values:
0. Marks a successful completion.1. Failure caused by an invalid argument.2. Failure resulting in a usage message, usually because an argument is missing.
Linux set Command Options
The set command provides an extensive list of options that can be combined.
Most options have a corresponding -o flag that can be used to invoke the option. The table below lists all options and their respective alternative form using the -o flag syntax.
| Options | -o flags | Description |
|---|---|---|
-a | -o allexport | Marks all created or modified variables or functions for export. |
-b | -o notify | Alerts the user upon background job termination. |
-e | -o errexit | Instructs a shell to exit if a command fails, i.e., if it outputs a non-zero exit status. |
-f | -o noglob | Disables filename generation (globbing). |
-h | -o hashall | Locates and saves function commands when a function is defined. The -h option is enabled by default. |
-k | -o keyword | Places all assignment arguments in the environment for a command, not just those preceding the command name. |
-n | -o noexec | Reads commands but doesn't execute them. |
-m | -o monitor | Displays a message when a task completes. |
-p | -o privileged | Disables the $ENV file processing and shell functions importing. The -p option is enabled by default when the real and effective user IDs don't match. Turning it off sets the effective uid and gid to the real uid and gid. |
-t | -o onecmd | Reads one command and then exits. |
-u | -o nounset | Treats unset or undefined variables as an error when substituting (during parameter expansion). Does not apply to special parameters such as wildcard * or @. |
-v | -o verbose | Prints out shell input lines while reading them. |
-x | -o xtrace | Prints out command arguments during execution. |
-B | -o braceexpand | Performs shell brace expansion. |
-C | -o noclobber | Prevents overwriting existing regular files by output redirection. By default, Bash allows redirected output to overwrite existing files. |
-E | -o errtrace | Causes shell functions to inherit the ERR trap. |
-H | -o histexpand | Enables style history substitution. The option is on by default when the shell is interactive. |
-P | -o physical | Prevents symbolic link following when executing commands. |
-T | -o functrace | Causes shell functions to inherit the DEBUG trap. |
-- | n/a | Assigns the remaining arguments to the positional parameters. If there are no remaining arguments, unsets the positional parameters. |
- | n/a | Assigns any remaining arguments to the positional parameters. Turns off the -x and -v options. |
| n/a | -o emacs | Uses and emacs-style line editing interface. |
| n/a | -o history | Enables command history. |
| n/a | -o ignoreeof | The shell doesn't quit upon reading the end of file. |
| n/a | -o interactive-comments | Allows comments in interactive commands. |
| n/a | -o nolog | Does not record function definitions in the history file. |
| n/a | -o pipefail | The return value of a pipeline is the status of the last command that had a non-zero status upon exit. If no command had a non-zero status upon exit, the value is zero. |
| n/a | -o posix | Causes Bash to match the standard when the default operation differs from the Posix standard. |
| n/a | -o vi | Uses a line editing interface similar to vi. |
Linux set Command Examples
This section lists examples of the most common uses of the set command.
Using the set Command Without Options
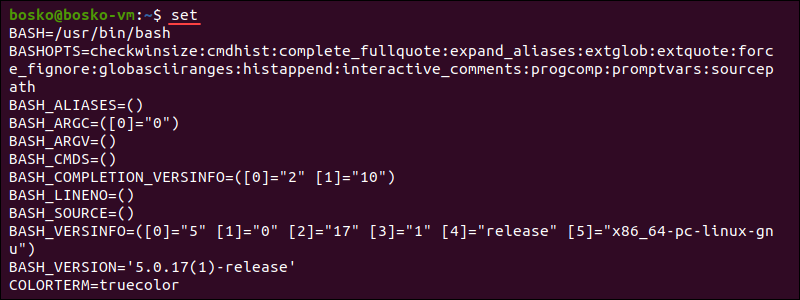
Running the command without options or arguments outputs a list of all settings - the names and values of all shell variables and functions. Since the list is very long, you can scroll through it using the Page Up and Page Down keys.
Following is an example of a partial set command output:
Script Debugging
The set command is especially handy when you are trying to debug your scripts. Use the -x option with the set command to see which command in your script is being executed after the result, allowing you to determine each command's result.
The following example demonstrates how to debug scripts with set -x. Follow the steps below:
1. Run set -x:
set -x2. Use your favorite text editor (we use the vi editor) to create a script. We created a simple loop that allows us to see the -x option effects:
x=10
while [ $x -gt 0 ]; do
x=$[ $x-1 ]
echo $x
sleep 2
done3. Make sure to chmod the script to make it executable. This step is always mandatory before running a script. The syntax is:
chmod +x [script-name.sh]4. Execute the script. The syntax is:
./[script-name.sh]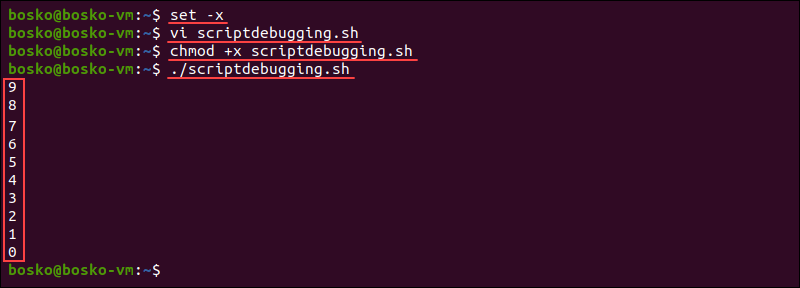
The output prints one line at a time, runs it, shows the result if there is one, and moves on to the next line.
Another way to enable debugging is to place the -x flag on the shebang line of the script:
#!/bin/bash -xScript Exporting
Automatically export any variable or function created using the -a option. Exporting variables or functions allows other subshells and scripts to use them.
Enable script exporting by running the following command:
set -aThe following example shows how script exporting works. Follow the steps below:
1. Create a new script using your editor of choice. For example:
one=1
two=2
three=3
four=4
/bin/bashThe /bin/bash argument marks the start of a new shell.
2. Check if the script works in a new shell:
echo $one $two $three $four

The output proves that the function we created was exported and works even when starting a new shell.
Exit When a Command Fails
Use the -e option to instruct a script to exit if it encounters an error during execution. Stopping a partially functional script helps prevent issues or incorrect results.
Create a script with the following contents to test this option:
#!/bin/bash
set -e
cat nonexistingfile
echo "The end"

In the example above, the script encounters an error when trying to show the contents of nonexistingfile because that file doesn't exist, causing it to exit at that point. Thus, the final echo command isn't executed.
Note: You can use the cat command to show a file's contents in a terminal window.
Prevent Data Loss
The default Bash setting is to overwrite existing files. However, using the -C option configures Bash not to overwrite an existing file when output redirection using >, >&, or <> is redirected to that file.
For example:
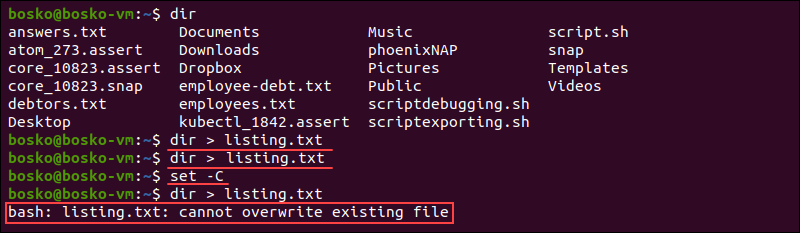
Bash first allows us to overwrite the listing.txt file. However, after running the set -C command, Bash outputs a message stating that it cannot overwrite an existing file.
Report Non-Existent Variables
The default setting in Bash is to ignore non-existent variables and work with existing ones. Using the -u option prevents Bash from ignoring variables that don't exist and makes it report the issue.
For example, the following script doesn't contain the set -u command and Bash ignores that $var2 isn't defined.
#!/bin/bash
var1="123"
echo $var1 $var2
The output contains only $var1.

However, changing the script and adding the set -u command prevents Bash from ignoring the problem and reports it:
#!/bin/bash
set -u
var1="123"
echo $var1 $var2

Set Positional Parameters
The set command can also assign values to positional parameters. A positional parameter is a shell variable whose value is referenced using the following syntax:
$[N]The [N] value is a digit that denotes the position of the parameter. For example, $1 is the first positional parameter, $2 is the second parameter, etc.
For example:
set first second thirdRunning the command above sets first to correspond to the $1 positional parameter, second to $2, and third to $3. Check this with the echo command:
echo $2
Unset positional parameters by running:
set --Split Strings
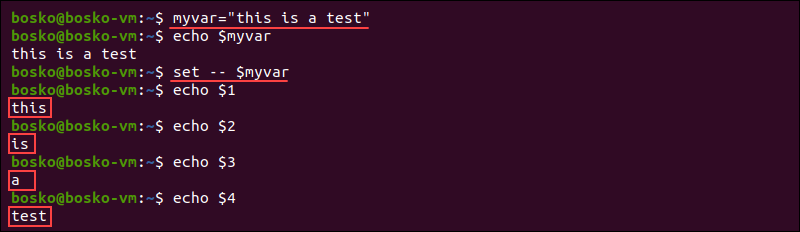
Use the set command to split strings based on spaces into separate variables. For example, split the strings in a variable called myvar, which says "This is a test".
myvar="This is a test"
set -- $myvar
echo $1
echo $2
echo $3
echo $4
Use this option to extract and filter out information from the output of a command, similar to what the awk command does.
Set allexport and notify Flags
The -o allexport flag allows you to automatically export all subsequently defined variables, while the -o notify flag instructs the shell to print job completion messages right away.
To set the flags, run:
set -o allexport -o notifyIn the following example, we see that the shell notifies you upon background job completion since the script was exported:

Note: If you want to run a process in the background, add the ampersand (&) symbol at the end of the command.
Conclusion
You now know what the set command is and how you can use it in Linux. Test out the different options to better understand the command and maximize your control of the Linux environment used by different packages.
If Bash is an interesting topic for you, check out our comprehensive tutorial on Bash Functions: How to Use Them.